 |
|
 |
NozzleFloQ1D is a CFD-tool for the numerical analysis of subsonic, transsonic and supersonic
quasi-1 dimensional inviscid nozzle flows. The non-dimensionalized Euler equations are cast
in strong conservation form and are explicitly solved using a finite-difference discretisation.
Time stepping is done using MacCormack's technique. A second order artificial dissipation
scheme is used to improve the resolution of shocks for flows with discontinuites. Damping is
controlled by an evaluation of the local pressure gradient. A 2nd order extrapolation of the
computed interior values is used at the in- and outflow boundaries. This program, coded in C, is based on
the method described in John D. Anderson's book "CFD: The Basics with Applications", which
I highly recommend to newcomers to the field of CFD.
References:
- Anderson, J.D.: "CFD: The Basics with Applications", McGraw-Hill, 1995.
- Haenel, D.: "Mathematische Stroemungslehre", AIA RWTH Aachen, 2000.
- Laney, C.B.: "Computational Gas Dynamics", Cambridge University Press, 1998.
|
The quasi-1D flow through a laval nozzle with a pressure ratio of pe/p0 = 0.016
is presented here.
An axial discretization of 31 equally-space nodes is used and the second order artificial dissipation
is set to zero.
A fully converged solution is achieved after less than 1500 iterations.
The results are presented as MS Excel diagrams of the average density residual and the
non-dimensional primitive variables along the nozzle axis.
|
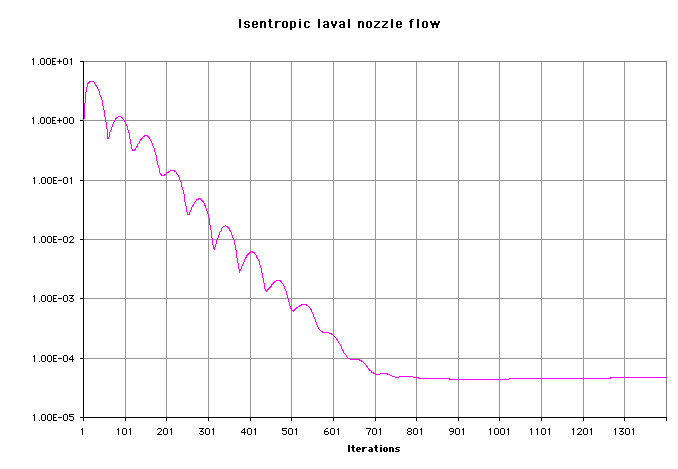
Logarithmic plot of the average density residual during the 1400 iterations shows a reduction by
5 orders of magnitude.
|
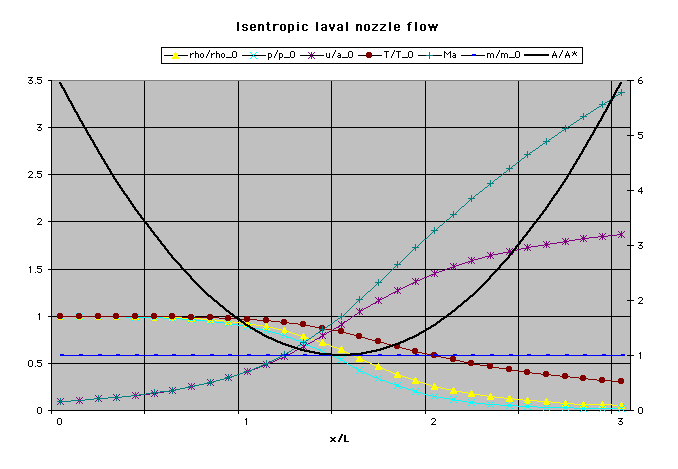
The steady-state results for the non-dimensionalized primitive variables are shown.
|
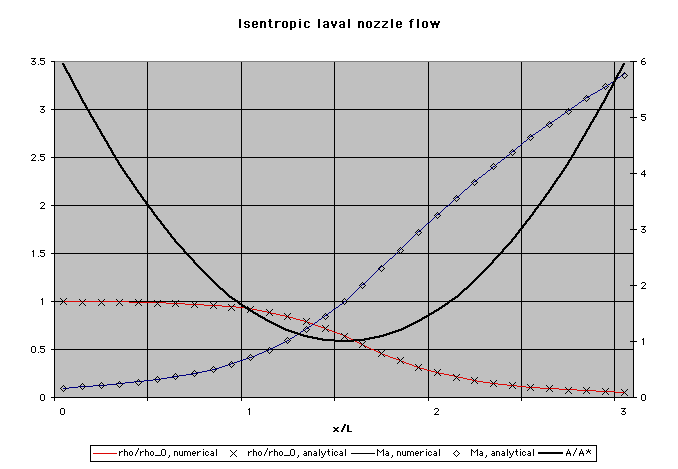
A comparison of the computed mach-number and density distributions along the nozzle axis with
analytical results for an isentropic laval nozzle flow. The hollow symbols are the analytical
values, which are in excellent agreement with the numerically computed values, represented by
the colored lines.
Top
|
The quasi-1D flow through a laval nozzle with a pressure ratio of pe/p0 = 0.6784
is presented here. An axial discretization of 61 equally-space nodes is used and the second order
artificial dissipation is set at a value of 0.2. A fully converged solution is achieved after 4500
iterations. Total runtime for the 4500 iterations was just over 18 minutes on a PowerMac with a 266MHz G3 processor.
The results are presented as MS Excel diagrams of the average density residual and the
non-dimensional primitive variables along the nozzle axis.
|
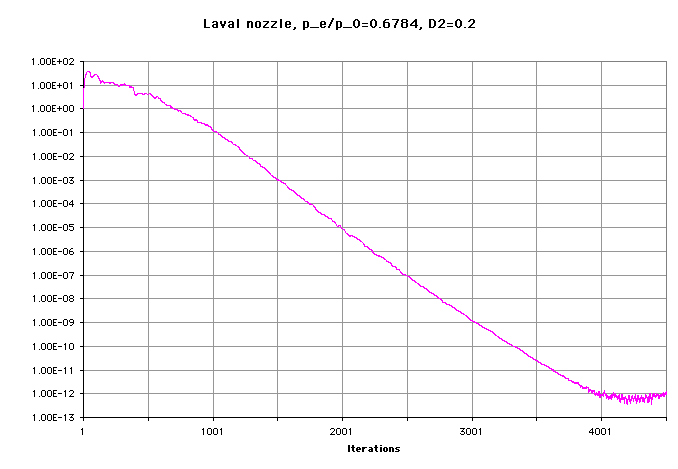
Logarithmic plot of the average density residual during the 4500 iterations shows a reduction by
13 orders of magnitude.
|
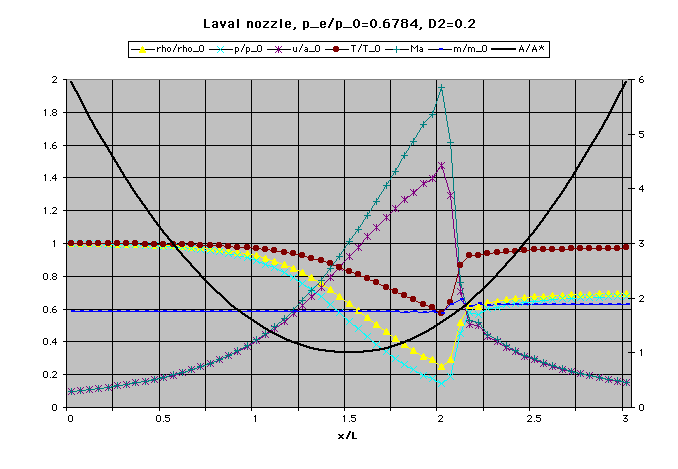
The steady-state results for the non-dimensionalized primitive variables are shown. Note the sharp
resolution of the shock with the associated unwanted but necessary slight increase in massflow.
The reason for this lies in the artificial viscosity necessary to achieve a good resolution of the
flowfield discontinuity. A good educational exercise could be to asses the impact of varying the
parameter of the dissipation term on shock resolution and massflow.
|
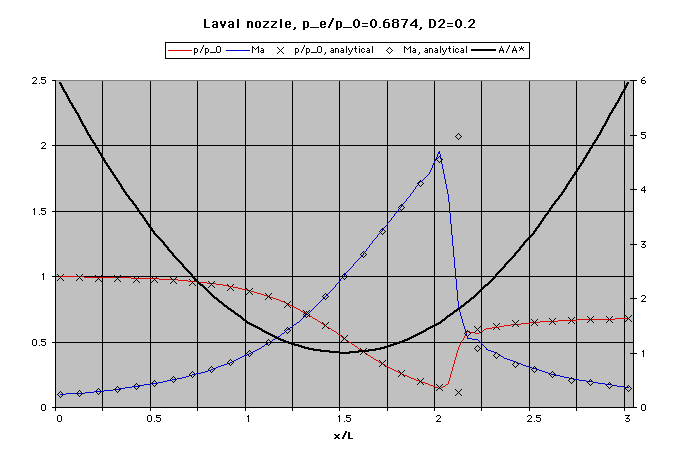
A comparison of the computed mach-number and pressure distributions along the nozzle axis with
analytical results for a nozzle pressure ratio of pe/p0 = 0.6784.
Top
|
|
|
 |


