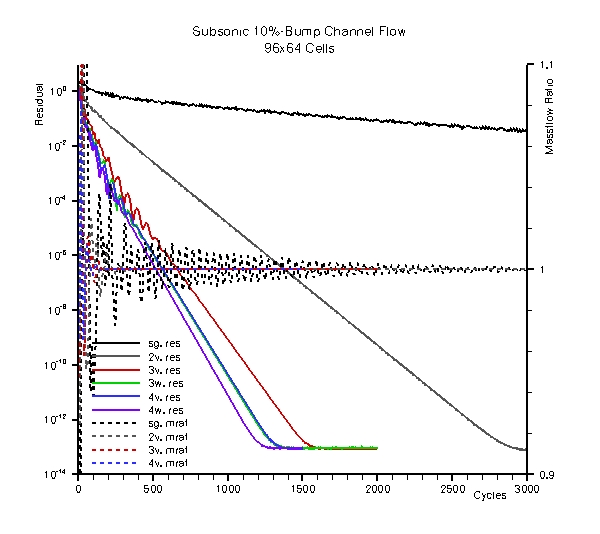
Comparative plot of the density residuals and the mass flow ratio across the channel for the various solver runs. The single-grid computations show a very poor rate of convergence in terms of the density residual and still exhibits fluctuations in the mass flow ratio after 3000 cycles. A significant improvement can already be achieved by using a 2v-multigrid cycle, which leads to a bottoming out of the density residual after 3000 cycles. Using a 3v-multigrid cycle results in a fully converged solution after 1600 cycles, while machine accuracy is achieved after 1400 cycles for both a 3w- and a 4v-cycle. For the 4w-cycle a fully converged solution can be reached after 1300 cycles, which is the lowest number of iterations of all of the multigrid cycles tested.

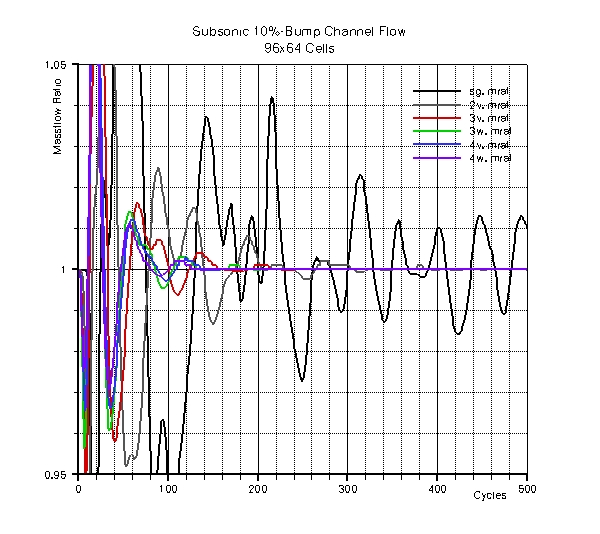
The benefit of running this case with multigrid also becomes evident when looking at the evolution of the mass flow-ratio across the channel during the first 500 cycles of the various computations. The single grid run shows strong oscillations which can be damped out much earlier using multigrid acceleration. Much like the situation for the overall rate of convergence described above, using more grid levels as well as using a w- instead of a v-cycle tends to speed up the damping out of oscillations in the mass flow-ratio, with the 4w-multigrid cycle leading to a constant value after only about 150 cycles.

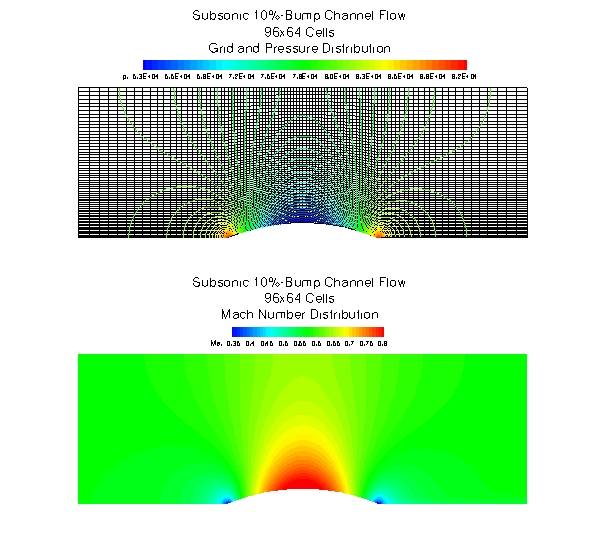
The 2D-contour plot of the mach number distribution shows completely subsonic flow through the channel, with only a slight acceleration on the top of the bump. The top image shows iso-lines of pressure superimposed on the grid of the finest level used in this study.

This table lists details pertaining to the convergence and run times for the various cases. The value in parentheses in the cycle column is the iteration at which the density residual drops below a value of 1e-13 for the first time. This convergence criteria is somewhat arbitrary but does allow for a fairly accurate comparison of the time-to-convergence as the final density residual fluctuates around a value of 9e-14 for all cases. For all cases the physically relevant properties mass flow and mass flow ratio have reached identical values at convergence. Of interest is the time to convergence, which is a product of the average runtime per cycle and the iteration number at which the density residual reaches 1e-13. It shows - with one notable exception - that the improved convergence rate of w-cycles over v-cycles and of increasing the number of multigrid levels also translates to an overall increase in efficiency, i.e. runtime to convergence. However the 4w-cycle does seem to be close to the optimum in terms of efficiency, as the improvement over the 4v-cycle is relatively small. The notable exception mentioned is the 3w-cycle, which is slightly more expensive than the 3v-cycle in terms of compute time. A possible explanation for this is that here three rather expensive Runge-Kutta cycles on the 2nd finest grid level need to be performed per cycle, while only two are required for the 3v-cycle. The extra RK-cycle on the 3rd finest grid level for the 4w-cycle versus the 4v-cycle on the other hand seems to be less costly and more effective in improving convergence, making the time to convergence for the 4w-cycle the quickest of the cases tested here.